Question

A survey of 32 different gas stations in Texas found the average price of gasoline to be $3.19 a gallon with a sample standard deviation of $0.096. Let μ be the true average price of gasoline price in Texas. The survey company claimed that gasoline in Texas was significantly lower than the national average $3.26 a gallon. The alernative hypothesis to test the claim is H 1 : μ <$3.26. Calculate the test statistic.

Answer 1

The value of test statistic is -4.1247

Explanation:

We are given the following in the question:

Population mean, μ = $3.26 a gallon

Sample mean,
`\bar{x}` = $3.19 a gallon

Sample size, n = 32

Sample standard deviation, σ = $0.096

First, we design the null and the alternate hypothesis

`H_(0): \mu = 3.26\text{ dollars a gallon}\\H_A: \mu < 3.26\text{ dollars a gallon}`

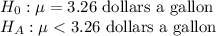
We use one-tailed t test to perform this hypothesis.

Formula:

`t_(stat) = \displaystyle\frac{\bar{x} - \mu}{(\sigma)/(√(n)) }`

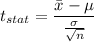
Putting all the values, we have

`t_(stat) = \displaystyle(3.19 - 3.26)/((0.096)/(√(32)) ) = -4.1247`

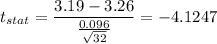
Thus, the value of test statistic is -4.1247