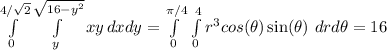Question

Convert the integral below to polar coordinates and evaluate the integral.

Lim(0→4/√2) ∫ Lim(y→√(16−y2)) ∫ xy dxdy

Instructions:
Enter the limits of integration and evaluate the integral to find the volume.

Answer 1

`\int\limits_(0)^(4/√(2))\int\limits_(y)^(√(16-y^2)) xy \, dxdy = \int\limits_(0)^(\pi/4) \, \int\limits_(0)^(4) r^3 cos(\theta)\sin(\theta) \,\, drd\theta = 16`

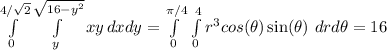
Explanation:

We are trying to evaluate this integral.

`\int\limits_(0)^(4/√(2))\,\,\int\limits_(y)^(√(16-y^2)) xy \,\,dxdy`

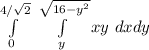
The first thing that we have to do is understand this region in the plane.

`\{ (x,y) \in \mathbb{R} : 0\leq y \leq (4)/(√(2)) \,\, , y \leq x \leq \, √(16-y^2) \}`

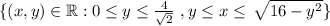
If you graph it looks something like the photo I join.

Now we need to describe that same region in polar coordinates.

That same region in polar coordinates would be

`\{ (r,\theta) : \,\, 0 \leq \theta \leq (\pi)/(4) \,\,\, 0\leq r \leq 4 \}`

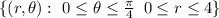
Now remember that when we do the polar transformation we use the following formula

`\int\limits_(a)^(b) \, \int\limits_(c)^(d) f(x,y) \,dxdy = \int\limits_(\theta_1)^(\theta_2) \, \int\limits_(r_1)^(r_2) r* f(rcos(\theta),rsin(\theta)) \,drd\theta`

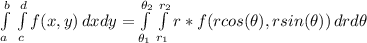
Then our integral would be

`\int\limits_(0)^(4/√(2))\int\limits_(y)^(√(16-y^2)) xy \, dxdy = \int\limits_(0)^(\pi/4) \, \int\limits_(0)^(4) r^3 cos(\theta)\sin(\theta) \,\, drd\theta = 16`