Question

Based on data a coffee shop owner has collected, she believes that 12% of her customers will buy a cookie to go with their coffee and that these purchases are independent. One day as she’s getting ready to close, 6 customers enter the shop and she has only 2 cookies left. What is the probability that no more than 2 of these last 6 customers will want a cookie?

Answer 1

Probability that no more than 2 of these last 6 customers will want a cookie is 0.974.

Explanation:

We are given that Based on data a coffee shop owner has collected, she believes that 12% of her customers will buy a cookie to go with their coffee and that these purchases are independent.

One day as she’s getting ready to close, 6 customers enter the shop and she has only 2 cookies left.

The above situation can be represented through Binomial distribution;

`P(X=r) = \binom{n}{r}p^(r) (1-p)^(n-r) ; x = 0,1,2,3,.....`

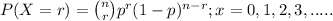
where, n = number of trials (samples) taken = 6 customers

r = number of success = no more than 2

p = probability of success which in our question is % of

customers who will buy a cookie, i.e; 12%

LET X = Number of customers who will want a cookie

So, it means X ~ Binom(
`n=6, p=0.12`)

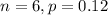Now, probability that no more than 2 of these last 6 customers will want a cookie is given by = P(X
`\leq` 2)

P(X
`\leq` 2) = P(X = 0) + P(X = 1) + P(X = 2)

=
`\binom{6}{0}* 0.12^(0) * (1-0.12)^(6-0)+ \binom{6}{1}* 0.12^(1) * (1-0.12)^(6-1)+ \binom{6}{2}* 0.12^(2) * (1-0.12)^(6-2)`

=
`1 * 1 * 0.88^(6) +6 * 0.12 * 0.88^(5) +15 * 0.12^(2) * 0.88^(4)`

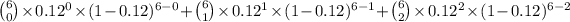
= 0.974

Hence, the probability that no more than 2 of these last 6 customers will want a cookie is 0.974.