Question

Consider light from a laser that has wavelength of 632.8 nm in air. As the light travels from the air into Lucite (index of refraction 1.50) calculate its (a) frequency in air, (b) wavelength in Lucite and (c) speed in Lucite. Put all three answers labeled with (a), (b) and (c) in the box below.

Answer 1

Solution of each part is given below .

Step-by-step explanation:

Given :

Wavelength of laser in air is ,
`\lambda=632.8\ nm` .

We know its velocity in air is ,
`c=3* 10^8\ m/s` .

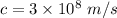So , its frequency is ,

`f=(c)/(\lambda)\\\\f=(3* 10^8)/(632.8* 10^(-9))\\\\f=4.74* 10^(14)\ s^(-1)`

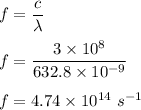
We know , frequency is source dependent only and since the source is same so frequency will be same and equal to
`f=4.74* 10^(14)\ s^(-1)` .

Therefore , its velocity in Lucite is :

`v=(c)/(\mu)\\\\v=(3* 10^8)/(1.5)\\\\v=2* 10^8\ m/s`

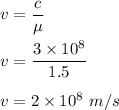
New wavelength is :

`\lambda'=(v)/(f)\\\\\lambda'=(2* 10^8)/(4.74* 10^(14))\\\\\lambda'=4.219* 10^(-7)\ m\\\\\lambda'=421.9\ nm`

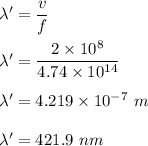
Hence , this is the required solution .