Question

Help Me on this!!



`\\ \\`
​

Answer 1

`\qquad\qquad\huge\underline{{\sf Answer}}`

Measure of Angle 3 is given, that is : Angle 3 = 74°

And the lines a and b are parallel, similarly line c and d are parallel to each other as well.

Now, let's just use property of angles on parallel lines to find measure of each angle we have been asked.

`\qquad \tt \dashrightarrow \: \angle1 = \angle3 = 74 \degree`

[ By Corresponding Angle pair ]

・ ．━━━━━━━†━━━━━━━━━．・

`\qquad \tt \dashrightarrow \: \angle7 + \angle3 = 180 \degree`

[ By Linear Pair ]

`\qquad \tt \dashrightarrow \: \angle7 = 180 - \angle3`

`\qquad \tt \dashrightarrow \: \angle7 = 180 - 74`

`\qquad \tt \dashrightarrow \: \angle7 = 106 \degree`

・ ．━━━━━━━†━━━━━━━━━．・

`\qquad \tt \dashrightarrow \: \angle8 = \angle3 = 74 \degree`

[ By Vertical opposite angle pair ]

・ ．━━━━━━━†━━━━━━━━━．・

`\qquad \tt \dashrightarrow \: \angle7 = \angle11 = 106 \degree`

[ opposite angles of a Parallelogram ]

・ ．━━━━━━━†━━━━━━━━━．・

`\qquad \tt \dashrightarrow \: \angle13= \angle3 = 74 \degree`

[ by Corresponding Angle pair ]

Answer 2

So here we are given that a || b and c || d, so the quadrilateral formed by the intersection of the four lines is just a parallelogram, so recall the property of parallelogram that parallelogram's opposite angles are always equal and the interior angles on the same side add up to 180°, and the property of angles that the alternate angles are always equal (that's angles Like in the Shape Z) and vertically opposite angles are equal (like in shape of X) and the property of linear pair i.e the sum of all angles on a plane line is 180°.

Now, as angles 3 and 7 are on a line d, so their sum will just be 180°, by property of linear pair

`{:\implies \quad \sf m\angle 3+m\angle 7=180^(\circ)}`

`{:\implies \quad \sf m\angle 7+74^(\circ)=180^(\circ)}`

`{:\implies \quad \sf m\angle 7=180^(\circ)-74^(\circ)}`

`{:\implies \quad \boxed{\bf{m\angle 7=106^(\circ)}}}`

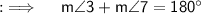
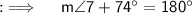
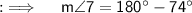
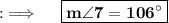
Also, as angles 8 and 3 are vertically opposite angles, so they will be same, so we have

`{:\implies \quad \boxed{\bf{m\angle 8=74^(\circ)}}}`

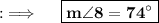
Now also, angle 7 and angle 11 are opposite angles of the parallelogram, so they will be equal, so we have :

`{:\implies \quad \boxed{\bf{m\angle 11=106^(\circ)}}}`

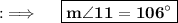
Also, the interior angles on same side of Parallelogram add upto 180°, so we can have ;

`{:\implies \quad \sf m\angle 11+m\angle 13=180^(\circ)}`

`{:\implies \quad \sf m\angle 13+106^(\circ)=180^(\circ)}`

`{:\implies \quad \sf m\angle 13=180^(\circ)-106^(\circ)}`

`{:\implies \quad \boxed{\bf{m\angle 13=74^(\circ)}}}`

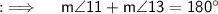
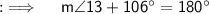
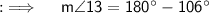
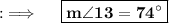
Also, Opposite angles of Parallelogram are equal, so angle 6 will be equal to angle 13, so angle 6 will be 74° and we also know the Vertically Opposite angles are equal. So, for angle 1 we have

`{:\implies \quad \boxed{\bf{m\angle 1=74^(\circ)}}}`

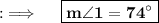
Now, we are end with the conclusion :

• 
  `{\bf{m\angle 1=74^(\circ)}}`
• 
  `{\bf{m\angle 7=106^(\circ)}}`
• 
  `{\bf{m\angle 8=74^(\circ)}}`
• 
  `{\bf{m\angle 11=106^(\circ)}}`
• 
  `{\bf{m\angle 13=74^(\circ)}}`