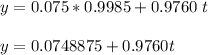Answer:
a)
The wave amplitude A = 0.075 m
Angular frequency = 12.57 rad/s
Period = 0.5 s
Wavelength = 6.0 m
Wave number = 1.0475 m⁻¹
b)
The wave function describing the wave =
![y(x,t) = 0.075 m \ cos \ [(1.0475 \ rad/m)x - (12.57 \ rad/s) t]](https://img.qammunity.org/2021/formulas/physics/college/q69j2s5zzjv1fozfvwg1s2t6rpnxj83lhw.png)
c) y= 0.0748875 + 0.9760 t
Step-by-step explanation:
a)
The wave amplitude A = 0.075 m
Angular frequency (ω) = 2πf
= 2× π× 2
= 12.57 rad/s
Period
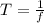
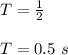
Wavelength
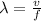
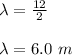
Wave number

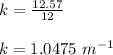
b)
The wave equation describing the wave can be illustrated as:
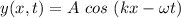
![y(x,t) = 0.075 m \ cos \ [(1.0475 \ rad/m)x - (12.57 \ rad/s) t]](https://img.qammunity.org/2021/formulas/physics/college/q69j2s5zzjv1fozfvwg1s2t6rpnxj83lhw.png)
c)
The equation for the displacement as a function of time of the particle at and of a point at 3.00 m is as follows:
![y= 0.075 \ cos \ [(1.0475 *3) - (12.57 ) t]](https://img.qammunity.org/2021/formulas/physics/college/q3u5y3794zju27y3bulg67z3j86kmnfhgy.png)