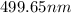Answer:
The dominant wavelength of the sun is
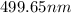
Step-by-step explanation:
Wien's law is defined as:
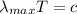 (1)
(1)
Where
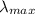 is the maximum wavelength, c is the Wien's constant and T is the temperature.
is the maximum wavelength, c is the Wien's constant and T is the temperature.
Therefore,
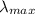 can be isolated from equation 1.
can be isolated from equation 1.
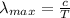 (2)
(2)
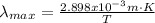
Notice that it is necessary to express the Wien's constant in units of meters
 ⇒
⇒
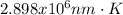
Finally, equation 2 can be used:
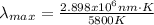
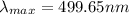
Hence, the dominant wavelength of the sun is