Answer:
3.27 turns
Step-by-step explanation:
To find how many turns (θ) will the stone make before coming to rest we will use the following equation:
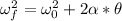
Where:
 : is the final angular velocity = 0
: is the final angular velocity = 0
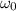 : is the initial angular velocity = 71.150 rpm
: is the initial angular velocity = 71.150 rpm
α: is the angular acceleration
First, we need to calculate the angular acceleration (α). To do that, we can use the following equation:
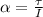
Where:
I: is the moment of inertia for the disk
τ: is the torque
The moment of inertia is:
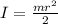
Where:
m: is the mass of the disk = 105.00 kg
r: is the radius of the disk = 0.297 m
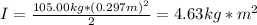
Now, the torque is equal to:
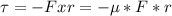
Where:
F: is the applied force = 46.650 N
μ: is the kinetic coefficient of friction = 0.451

The minus sign is because the friction force is acting opposite to motion of grindstone.
Having the moment of inertia and the torque, we can find the angular acceleration:
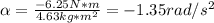
Finally, we can find the number of turns that the stone will make before coming to rest:
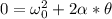
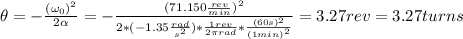
I hope it helps you!