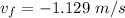Question

A ball is attached to one end of a wire, the other end being fastened to the ceiling. The wire is held horizontal, and the ball is released from rest (see the drawing). It swings downward and strikes a block initially at rest on a horizontal frictionless surface. Air resistance is negligible, and the collision is elastic. The masses of the ball and block are, respectively, 1.6 kg and 2.5 kg, and the length of the wire is 1.35 m. Find the velocity (magnitude and direction) of the ball (a) just before the collision, and (b) just after the collision.

Answer 1

the velocity (magnitude and direction) of the ball) just before the collision is
`v_i = 5.144 \ m/s`

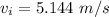
The velocity (magnitude and direction) of the ball) just after the collision is
`v_f = - 1.129 \ m/s`

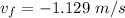
Step-by-step explanation:

According to the law of conservation of energy;

`m__(ball)} gh = (1)/(2)m__(ball)}v_i^2\\\\2* m__(ball)} gh = m__(ball)}v_i^2\\\\v_i^2 = (2*m_(ball)gh)/(m_(ball))\\\\v_i^2 = 2gh\\\\v_i = √(2gh) \\\\v_i = √(2*9.8*1.35)\\\\`

`v_i = 5.144 \ m/s`

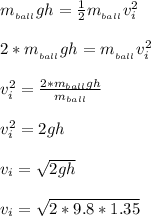
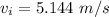
Thus; the velocity (magnitude and direction) of the ball) just before the collision is
`v_i = 5.144 \ m/s`

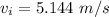
Since, Air resistance is negligible, and the collision is elastic.

The equation for the conservation of momentum and energy can be expressed as:

`v_f = [(m_1 -m_2)/(m_1+m_2)]v_i\\\\v_f = [(m_(ball) -m_(block))/(m_(ball)+m_(block))]v_i\\\\v_f = [(1.6 -2.5)/(1.6+2.5)]*5.144\\\\`

`v_f = - 1.129 \ m/s`

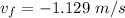
The velocity (magnitude and direction) of the ball) just after the collision is
`v_f = - 1.129 \ m/s`