Question

A process for a certain type of ore is designed to reduce the concentration of impurities to less than 2%. It is known that the standard deviation of impurities for processed ore is 0.6%. Let µ represent the mean impurity level, in percent, for ore specimens treated by this process. The impurity of 80 ore specimens is measured, and a test of the hypothesis H0: µ > 2 versus H1: µ < 2 will be performed.

a. If the test is made at the 1% level, what is the rejection region?

Answer 1

The rejection region is the area under the curve for every value of X below Xc=1.844.

Explanation:

We have a test hypothesis and we have to calculate the critical value Xc that delimitates the rejection region, being X the sample mean.

This is a left-tail test, so the value for z is z=-2.327.

The value for

`X_c=\mu+z\sigma/√(n)\\\\X_c=2-2.327*0.6/√(80)\\\\X_c=2-1.3962/8.944\\\\X_c=2-0.156\\\\X_c=1.844`

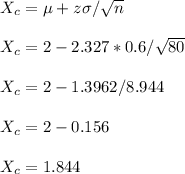
The rejection region is the area under the curve for every value of X below Xc=1.844.