Question

Computers require fans to keep them from overheating. Let T be the random variable representing the lifetime of a particular make of fan in hours. Assume that T follows an exponential distribution with parameter λ = 0.0003. (a) Find the proportion of computer fans which will give at least 10,000 hours of service. (b) If the fan is redesigned so that exponential lifetime distribution now has parameter λ = 0.00035, would you expect more fans or fewer fans to live for at least 10,000 hours?

Answer 1

a) 4.98% of computer fans which will give at least 10,000 hours of service.

b) 3.02% of computer fans which would give at least 10,000 hours of service, that is, fewer fans living for at least 10,000 hours.

Explanation:

Exponential distribution:

The exponential probability distribution, with mean m, is described by the following equation:

`f(x) = \mu e^(-\mu x)`

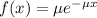
In which
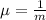`\mu = (1)/(m)` is the decay parameter.

The probability that x is lower or equal to a is given by:

`P(X < x) = \int\limits^a_0 {f(x)} \, dx`

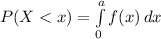
Which has the following solution:

`P(X < x) = 1 - e^(-\mu x)`

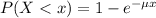
In this problem, we have that:

`\mu = \lambda = 0.0003`

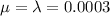
(a) Find the proportion of computer fans which will give at least 10,000 hours of service.

Either it gives less 10,000 hours of service, or it gives at least 10,000. The sum of the probabilities of these events is decimal 1. So

`P(X < 10000) + P(X \geq 10000) = 1`

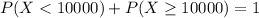
We want
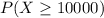`P(X \geq 10000)`. So

`P(X \geq 10000) = 1 - P(X < 10000)`

`P(X < 10000) = 1 - e^(-0.0003*10000) = 0.9502`

`P(X \geq 10000) = 1 - 0.9502 = 0.0498`

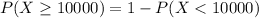
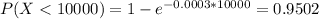
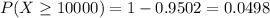
4.98% of computer fans which will give at least 10,000 hours of service.

(b) If the fan is redesigned so that exponential lifetime distribution now has parameter λ = 0.00035, would you expect more fans or fewer fans to live for at least 10,000 hours?

Now
`\mu = \lambda = 0.00035`

`P(X \geq 10000) = 1 - P(X < 10000)`

`P(X < 10000) = 1 - e^(-0.00035*10000) = 0.9698`

`P(X \geq 10000) = 1 - 0.9698 = 0.0302`

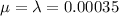
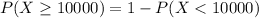
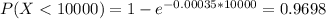
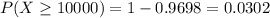
3.02% of computer fans which would give at least 10,000 hours of service, that is, fewer fans living for at least 10,000 hours.