Question

An object at rest on a flat, horizontal surface explodes into two fragments, one seven times as massive as the other. The heavier fragment slides 7.00 m before stopping. How far does the lighter fragment slide?

Answer 1

The distance the lighter fragments slides is 343 m

Step-by-step explanation:

Here, we have

Let the mass of the heavier fragments be m₁

Let the distance the heavy object slide be d₁

Let the mass of the lighter fragments be m₂

Let the final velocity of the heavier fragments be v₁

Let the final velocity of the lighter fragments be v₂

Let the distance the light object slide be d₂

The distance traveled by the heavy fragment = 7.00 m

Therefore since m₁ = 7 × m₂ we have

Initial total momentum = final total momentum

Since the initial total momentum = 0 we have

m₁·v₁ + m₂·v₂ = 0 or

7·m₂·v₁ = -m₂·v₂

∴ v₂ = 7·v₁

The net work done by the heavier block is

W
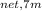`_(net, 7m)` = μk × m₁ × g × d₁ = 1/2×m₂×v₂²

Also v₁² = 2μk·g·d₁ and

v₂² = 2μk·g·d₂ so that since v₂ = 7·v₁ or v₁ = v₂/7 we get

(v₂/7)² = 2μk·g·d₁

So v₂²/49 = 2μk·g·d₁

or (2μk·g·d₂)/49 = 2μk·g·d₁

∴ d₂/49 = d₁

d₂ = d₁×49 = 7 × 49 = 343 m

The distance the lighter fragments slides = 343 m.