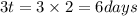Answer:
6 days
Step-by-step explanation:
We are given that
Half life,
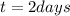
We have to find the time must elapse before the room is safe to enter.
Let maximum permissible level=
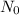
Radiation,
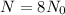
Let n be the number of half cycle
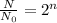
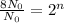
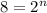
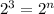
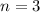
Time must elapse before the room is safe to enter=