Answer:
z= -2.93
|z| = |-2.93|=2.93there fore we accepted Alternative hypothesis
The calculated z =2.93 > 1.6 the tabulated value at 89% level of significance.
A school social worker is interested in testing the claim that less than 89% of teenagers graduate from high school.
Explanation:
Step(i)
Given sample of 380 teenagers and 320 of them graduated from high school
The proportion of sample is
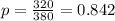
Given a school social worker is interested in testing the claim that less than 89% of teenagers graduate from high school
The population proportion 'P' = 0.89
Null hypothesis:- H₀: p= 0.89
Alternative hypothesis: H: p< 0.89
Step(ii)
The test statistic
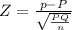
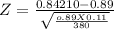
on calculation , we get
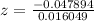
z = -2.93
|z| = |-2.93|=2.93
we will use 89% of level of z- score =1.6 (check normal diagram)
The calculated z =2.93 > 1.6 the tabulated value at 89% level of significance.
we rejected null hypothesis
we accepted alternative hypothesis
Conclusion:-
A school social worker is interested in testing the claim that less than 89% of teenagers graduate from high school.