Question

A fisherman notices that his boat is moving up and down periodically without any horizontal motion, owing to waves on the surface of the water. It takes a time of 2.90 s for the boat to travel from its highest point to its lowest, a total distance of 0.700 m . The fisherman sees that the wave crests are spaced a horizontal distance of 5.50 m apart.

Answer 1

wavelength
`\lambda` = 5.50 m

The period T = 5.80 s

The speed v = 0.948 m/s

Amplitude A of each wave = 0.350 m

Step-by-step explanation:

Since the wave crests is 5.50 m; then we can say that the distance from one peak to another is equal to a single wavelength;

SO; wavelength
`\lambda` = 5.50 m

Given that ; the time to travel from the highest point to the lowest point = 2.90 s

Thus
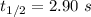`t_(1/2) = 2.90 \ s` ; which implies just only about half of one wavelength

The period for one wavelength T = twice of half of one wavelength which can be expressed as :

T =
`2 t_(1/2)`

T = 2 (2.90 s)

T = 5.80 s

The speed of the wave can be determined via the formula;

`v = (\lambda)/(T)\\\\v = (5.50 \ m)/(5.80 \ s)\\\\v = 0.948 \ m/s`

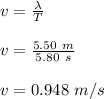
The amplitude A is half the distance because the distance illustrates the peak to peak vertical displacement of the wave ;

∴

A =
`(0.700 \ m)/(2)`

A = 0.350 m