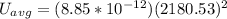Question

An instructor’s laser pointer produces a beam of light with a circular cross section of diameter 0.900 mm and a total power output of 4.00 mW. The beam size stays nearly constant when the instructor uses the laser pointer in the classroom. What is the amplitude E 0 of the electric field of the laser’s light? E 0 = N/C What is the amplitude B 0 of the magnetic field of the laser’s light? B 0 = T What is the average energy density u ave of the laser’s light? u ave J/m 3

Answer 1

`E_0 = 2180.53N/C.`

`B_0 = 7.27*10^(-6)T.`

`U_(avg) = 4.2*10^(-5)J/m^3.`

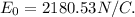
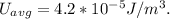
Step-by-step explanation:

The Intensity
`I` of the beam is

`I = P /A`

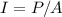
The diameter of the beam is 0.900mm; therefore, the area is

`A = \pi( (0.900*10^(-3))/(2) )^2`

`A = 6.36*10^(-7)m^2`

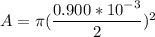
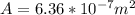
and since
`P = 4.00*10^(-3)W`, the intensity of the beam is

`I = (4.00*10^(-3)W)/(6.36*10^(-7)m^2)`

`\boxed{I = 6289.3W/m^2.}`

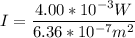
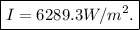
Now, the intensity
`I` is related to
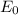`E_0` by the relation

`I = (E_0^2)/(2\mu_0 c)`

solving for
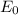`E_0` we get

`E_0 = √(2\mu_0 c I)`

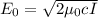
putting in the numbers we get:

`E_0 = \sqrt{2(1.26*10^(-6)) (3*10^8) (6289.3)}`

`\boxed{E_0 = 2180.53N/C.}`

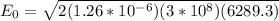
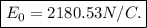
The amplitude of magnetic field
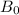`B_0` is related to
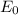`E_0` by

`B_0 = (E_0)/(c)`

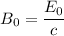
putting in numerical values we get:

`B_0 = (2180.53)/(3*10^8)`

`\boxed{B_0 = 7.27*10^(-6)T. }`

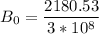
The average energy density of the laser light is

`U_(avg) = \epsilon_0 E_0^2`

`U_(avg) = (8.85*10^(-12)) (2180.53)^2`

`\boxed{U_(avg) = 4.2*10^(-5)J/m^3.}`