Question

Five years after 650 high school seniors graduated, 400 had a college degree and 310 were married. Half of the students with a college degree were married. What is the probability that a student has a college degree or is not married

Answer 1

Answer: 2/34

Explanation:

2/34 chance

Answer 2

The probability that a student has a college degree or is not married is 0.8308.

Explanation:

The information provided is:

Total number of high school seniors (N) = 650.

Number of seniors with a college degree (n (C)) = 400.

Number of seniors who were married, (n (M)) = 310.

Consider the Venn diagram below.

The probability of an event, say E, is the ratio of the favorable outcomes of E to the total number of outcomes of the experiment.

That is,

`P(E)=(n(E))/(N)`

Here,

n (E) = favorable outcomes of E

N = total number of outcomes of the experiment.

The probability of the union of two events is:

`P(A\cup B)=P(A)+P(B)-P(A\cap B)=(n(A)+n(B)-n(A\cap B))/(N)`

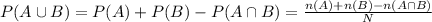
Compute the probability that a student has a college degree or is not married as follows:

`P(C\cup M^(c))=(n(C)+n(M^(c))-n(C\cap M^(c)))/(N)`

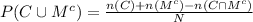
From the Venn diagram:

n (C) = 400

n (
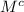`M^(c)`) = N - n (M) = 650 - 310 = 340

n (C ∩
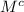`M^(c)`) = 200

The value of P (C ∪
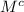`M^(c)`) is:

`P(C\cup M^(c))=(n(C)+n(M^(c))-n(C\cap M^(c)))/(N)=(400+340-200)/(650)=0.83077\approx0.8308`

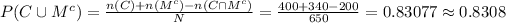
Thus, the probability that a student has a college degree or is not married is 0.8308.