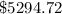Question

Daniel invests $2,037 in a retirement account with a fixed annual interest rate of 6% compounded 6 times per year. What will the account balance be after 16 years?

Answer 1

`\$5294.72`

Explanation:

GIVEN: Daniel invests
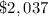`\$2,037` in a retirement account with a fixed annual interest rate of
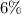`6\%` compounded
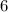`6` times per year.

TO FIND: What will the account balance be after
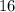`16` years

SOLUTION:

Amount invested by Daniel
`=\$2037`

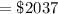
Annual interest rate
`=6\%`

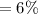
Total amount generated by compound interest is
`=P(1+(r)/(n))^n^t`

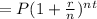
Here Principle amount
`P=\$2037`

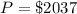
rate of interest
`r=6\%`

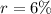
number of times compounding done in a year
`n=6`

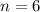
total duration of time
`nt=16\text{ years}`

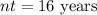
putting values we get

=
`2037(1+(6)/(6*100))^1^6`

`=2037((101)/(100))^1^6`

`=\$5294.72`

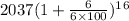
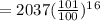
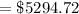
Hence the total balance after
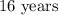`16\text{ years}` will be
`\$5294.72`