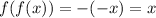Question

Confirm that f and g are inverses by showing that f(g(x)) = x and g(f(x)) = x.

f(x)=8/x and g(x)=8/x

Answer 1

f(x) and g(x) are inverses.

Explanation:

If we can view a function (f) as some kind of machine that takes in an input (x) and puts out an output (f(x)), we can view the inverse of the function as one that can "unwrap" the output and give us back the input. When you feed the output of f (f(x)) into its inverse function (usually written
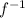`f^(-1)`), you get back out the original input, x. To give you an example: let's say we had a simple function, h, that just added 1 to its input. If we call our input x, we can write this in symbols as
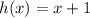`h(x)=x+1`. To find the inverse, we simply reverse the process. If we put in an input of 2 to h, we'll get out
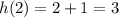`h(2)=2+1=3`. How can we get back to 2 from 3? By subtracting 1. So our inverse function would look like this for an input of 3:

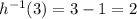`h^(-1)(3)=3-1=2`. And in general,
`h^(-1)(x)=x-1`.

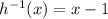Let's see if we get our original input back by feeding f(x) and g(x) into each other:

`f(g(x))=(8)/(8/x) =8\cdot(x)/(8) =x\\g(f(x))=(8)/(8/x) =8\cdot(x)/(8) =x`

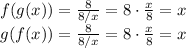
It checks out! f(x) and g(x) are inverses.

Something interesting about this particular example you might notice is that
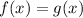`f(x)=g(x)`, so we could equivalently say that
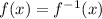`f(x)=f^(-1)(x)`, or in English: f is its own inverse! These kinds of functions are called involutions, and are of broad interest to mathematicians. Another elementary example of an involution is the function
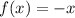`f(x)=-x`; for the input 1, applying the function twice gives us
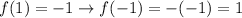`f(1)=-1\rightarrow f(-1)=-(-1)=1`, and in general,
`f(f(x))=-(-x)=x`