The length of KL is 103 feet, if ΔKLM, the measure of ∠M=90°, the measure of ∠L=55°, and LM = 59 feet.
Explanation:
The given is,
ΔKLM
∠M= 90°
∠L= 55°
LM = 59 feet
Step:1
The given triangle KLM is right angle triangle,
Ref the attachment,
Trigonometric metric ratio for triangle KLM is,
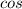 ∅ =
∅ =
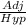
For the triangle KLM sin ∅ becomes,
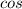 ∅ =
∅ =
 .........................(1)
.........................(1)
From the given,
∅ = 55°
LM = 59 feet
Equation (1) becomes,
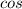 55° =
55° =
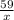
Where
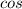 55° = 0.5736,
55° = 0.5736,
0.5736 =
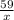
x =
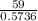
= 102.86
x = KL ≅ 103 feet
Step:2
Check for solution,
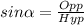
For triangle KLM,
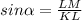
Substitute the values of LM and KL,
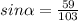
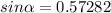

= 34.967
 ≅ 35°
≅ 35°
For right angle triangle,
90° = ∅ + α
= 55° + 35°
90° = 90°
Result:
The length of KL is 103 feet, if ΔKLM, the measure of ∠M=90°, the measure of ∠L=55°, and LM = 59 feet.