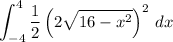Question

The base of a solid is bounded by x^2 + y^2 = 16. Cross sections perpendicular to the x-axis are right isosceles triangles with one leg located in the base. Which definite integral represents the volume of this solid?

Answer 1

The equation for the base is that of a circle, so the cross sections will have a leg of length equal to the vertical distance between its halves.

x² + y² = 16 ⇒ y = ±√(16 - x²)

⇒ length = √(16 - x²) - (-√(16 - x²)) = 2 √(16 - x²)

Cross sections with thickness ∆x have a volume of

1/2 length² ∆x = 1/2 (2 √(16 - x²))² ∆x = (32 - 2x²) ∆x

since they are isosceles triangles and so their bases and heights are equal.

Then the total volume would be (D)

`\displaystyle \int_(-4)^4 \frac12 \left(2 √(16-x^2)\right)^2 \, dx`