Question

(X^2+x-6)(2x^2+4x) factor completely

Answer 1

`2x\left(x-2\right)\left(x+3\right)\left(x+2\right)`

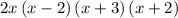
Explanation:

Lets go ahead and take a step by step approach to solving your problem.

First we must start by factoring
`x^2+x-6`.

To do this, we must break the expression into groups! Although I will also provide a definition to help you understand! For
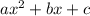`ax^2+bx+c` we need to find u, v >
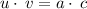`u\cdot \:v=a\cdot \:c` and
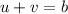`u+v=b` which we will group into
`\left(ax^2+ux\right)+\left(vx+c\right)`.

The values we have are...
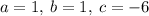`a=1,\:b=1,\:c=-6` and
`u\cdot v=-6,\:u+v=1`.

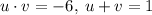Now we need the factors of 6 which are 1, 2, 3 and 6. We also need the negative factors which you get simply by multiplying the positives by -1 or just reversing them.

Now we need to check for every two factors if u + v = 1.

`\mathrm{Check}\:u=1,\:v=-6: \:u\cdot v=-6,\:u+v=-5 \Rightarrow \mathrm{False}`

`\mathrm{Check}\:u=2,\:v=-3: \:u\cdot v=-6,\:u+v=-1 \Rightarrow \mathrm{False}`

`\mathrm{Check}\:u=3,\:v=-2: \:u\cdot v=-6,\:u+v=1 \Rightarrow \mathrm{True}`

`\mathrm{Check}\:u=6,\:v=-1: \:u\cdot v=-6,\:u+v=5 \Rightarrow \mathrm{False}`

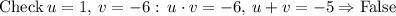
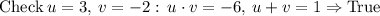
Therefore
`u=3,\:v=-2`.

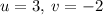Now we want to
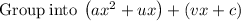`\mathrm{Group\:into\:}\left(ax^2+ux\right)+\left(vx+c\right)`. Which is
`\left(x^2-2x\right)+\left(3x-6\right)`.

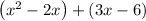Now we must factor x from
`x^2-2x`.

Lets apply the exponent rule of
`a^(b+c)=a^ba^c` which means
`x^2=xx`.

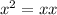Therefore we now have xx - 2x. Lets factor out the common term of x to get x(x - 2).

Now factor 3 out of
`3x-6`.

Rewrite 6 as 3 * 2.
`3x-3\cdot \:2`.

Now factor out the common term of 3 >
`3\left(x-2\right)`.

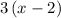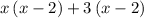`x\left(x-2\right)+3\left(x-2\right)` > Factor out the common term of x - 2 >
`\left(x-2\right)\left(x+3\right)`.

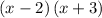Now lets factor
`2x^2+4x`.

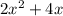Apply the previous exponent rule of
`a^(b+c)=a^ba^c` >
`x^2=xx` >
`2xx+4x`.

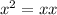Now rewrite 4 as 2 * 2 >
`2xx+2\cdot \:2x`.

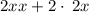Now factor out the common term of 2x to get 2x(x + 2).

Combine it all and we get
`2x\left(x-2\right)\left(x+3\right)\left(x+2\right)`.

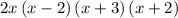Hope this helps!