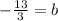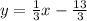Question

The equation of lineris y=-3x - 4. If line s runs perpendicular to line r and passes

through (4, -3), what would be the equation of lines?
CLEAR
CHECK

Answer 1

Slope-intercept form: y = mx + b

(m is the slope, b is the y-intercept or the y value when x = 0 --> (0, y) or the point where the line crosses through the y-axis)

For lines to be perpendicular, their slopes have to be negative reciprocals of each other. (flip the sign +/- and the fraction(switch the numerator and the denominator))

For example:

Slope = 2 or
`(2)/(1)`

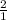
Perpendicular line's slope:
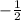`-(1)/(2)` (flip the sign from + to - , and flip the fraction)

Slope =
`-(2)/(5)`

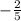
Perpendicular line's slope:
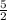`(5)/(2)` (flip the sign from - to +, and flip the fraction)

y = -3x - 4 The slope is -3, so the perpendicular line's slope is
`(1)/(3)`

Now that you know the slope, substitute/plug it into the equation,

y = mx + b

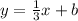`y=(1)/(3) x+b` To find b, plug in the point (4, -3) into the equation, then isolate/get the variable "b" by itself

`-3=(1)/(3) (4)+b`

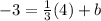
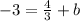`-3=(4)/(3) +b` Subtract 4/3 on both sides to get "b" by itself

`-3-(4)/(3) =b` To combine fractions, they must have the same denominator.

`((3)/(3) )(-3)-(4)/(3) =b`

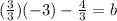
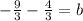`-(9)/(3) -(4)/(3) =b` Now combine the fractions

`-(13)/(3) =b`

`y=(1)/(3)x-(13)/(3)`