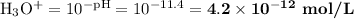Question

Ammonia has a Kb of 1.8 × 10−5. Find [H3O+], [OH−], pH, and pOH for a 0.310 M ammonia solution.

Answer 1

[H₃O⁺] = 4.3 × 10⁻¹² mol·L⁻¹; [OH⁻] = 2.4 × 10⁻³ mol·L⁻¹;

pH = 11.4; pOH = 2.6

Step-by-step explanation:

The chemical equation is

`\rm NH$_(3)$ + \text{H}$_(2)$O \, \rightleftharpoons \,$ NH$_(4)^(+)$ + \,\text{OH}$^(-)$`

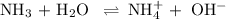
For simplicity, let's re-write this as

`\rm B + H$_(2)$O \, \rightleftharpoons\,$ BH$^(+)$ + OH$^(-)$`

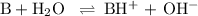
1. Calculate [OH]⁻

(a) Set up an ICE table.

B + H₂O ⇌ BH⁺ + OH⁻

0.310 0 0

-x +x +x

0.310-x x x

`K_{\text{b}} = \frac{\text{[BH}^(+)]\text{[OH}^(-)]}{\text{[B]}} = 1.8 * 10^(-5)\\\\(x^(2))/(0.100 - x) = 1.8 * 10^(-5)`

Check for negligibility:

`(0.310)/(1.8 * 10^(-5)) = 17 000 > 400\\\\x \ll 0.310`

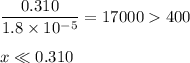
(b) Solve for [OH⁻]

`(x^(2))/(0.310) = 1.8 * 10^(-5)\\\\x^(2) = 0.310 * 1.8 * 10^(-5)\\x^(2) = 5.58 * 10^(-6)\\x = \sqrt{5.58 * 10^(-6)}\\x = \text{[OH]}^(-) = \mathbf{2.4 * 10^(-3)} \textbf{ mol/L}`

2. Calculate the pOH

`\text{pOH} = -\log \text{[OH}^(-)] = -\log(2.4 * 10^(-3)) = \mathbf{2.6}`

3. Calculate the pH

`\text{pH} = 14.00 - \text{pOH} = 14.00 - 2.6 = \mathbf{11.4}`

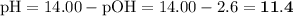
4 Calculate [H₃O⁺]

`\text{H$_(3)$O$^(+)$} = 10^{-\text{pH}} = 10^(-11.4) = \mathbf{4.2 * 10^(-12)} \textbf{ mol/L}`