Question

Part A: Suppose the direction of the force changes from a 48° angle with the

floor to a 70° angle with the floor. Determine the effect on the horizontal and
vertical components of the force. Give forces to the nearest hundredth of a
unit

Answer 1

Horizontal Component of Force decreases and Vertical Component Increases.

Explanation:

The rectangular components of a Force are given by:

Horizontal Component:

`F_(x)=Fcos(\theta)`

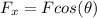
Vertical Component:

`F_(y)=Fsin(\theta)`

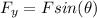
Here, F represents the magnitude of the Force and Θ is the angle between the Force F and the horizontal.

The initial value of Θ is 48 degrees. So under this condition the rectangular components will be:

`F_(x)=Fcos(48)=0.67F\\\\ F_(y)=Fsin(48)=0.74F`

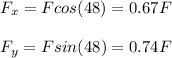
On increasing the angle to 70 degrees, the new rectangular components will be:

`F_(x)=Fcos(70)=0.34F\\\\ F_(y)=Fsin(70)=0.94F`

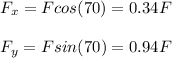
From the above calculations we can see that on increasing the angle made by the Force with floor from 48 degrees to 70 degrees:

• Horizontal component decreases from 0.67F to 0.34F
• Vertical component increases from 0.74F to 0.94F

If the value of Force F is known, the exact value of rectangular components can be calculated from the previous expressions.