Let
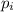 denote the vector starting at the origin and ending at the vertex
denote the vector starting at the origin and ending at the vertex
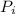 of the 12-gon. There is an angle of (360/12)º = 30º between consecutive vectors.
of the 12-gon. There is an angle of (360/12)º = 30º between consecutive vectors.
Recall that for any two vectors
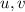 , we have
, we have

with
 the angle between the two vectors. Also recall that
the angle between the two vectors. Also recall that
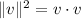
For
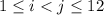 ,
,
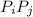 is the length of the vector
is the length of the vector
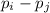 . So
. So
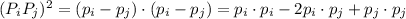
The 12-gon is inscribed in a circle of radius 1, which means each vector
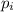 has length 1, and from this we have
has length 1, and from this we have
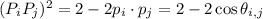
where
 is the angle between vectors
is the angle between vectors
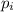 and
and
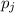 with
with
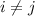 , and these angles are multiples of 30º.
, and these angles are multiples of 30º.
There are
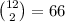 terms in the sum (from 12 total vertices, you take 2 at a time).
terms in the sum (from 12 total vertices, you take 2 at a time).
- 11 of these terms are the squared distances between consecutive vertices and separated by 30º, equal to
 ;
; - 10 of them are the squared distances between vertices that are two vertices apart, separated by 60º, equal to
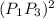 ;
; - 9 of them are the squared distances between vertices that are three vertices apart, separated by 90º, equal to
 ;
; - and so on, down to the 1 remaining uncounted squared distance between vertices that are ten vertices apart, separated by 330º,
 .
.
So we have

