Question

Underwater mortgages ~ A mortgage is termed "underwater" if the amount owed is greater than the value of the property that is mortgaged. Using a 2010 Rasmussen poll of 1020 homeowners, investigators calculated a 95% confidence interval for the actual proportion of homeowners in US that have mortgages that were underwater. The confidence interval is given by (0.2662, 0.3221). Which of the following statements are true? Select all the that apply.

a.A 99% confidence interval calculated using the same data will include more plausible values for the actual population proportion.
b.If the sample size had been double the sample size in the scenario above, then the 95% confidence interval would be half as wide as the one stated above.
c.If a different sample of the same size were to be selected, then there is a 95% chance that the new sample proportion will lie inside the confidence interval stated above.
d.If we took several samples of the same size as the scenario given above and constructed 95% confidence intervals for population proportion, then it is reasonable to expect 95% of these confidence intervals to contain the actual population proportion.
e.A 90% confidence interval for the population proportion calculated using the same data will be wider than the interval stated above.
If a different sample of the same size were to be selected and a 95% confidence interval constructed, then there is a 95% chance that the actual population proportion will lie inside the new confidence interval.

Answer 1

The correct statements are (a), (c) and (d).

Explanation:

The (1 - α)% confidence interval formula for population proportion (p) is as follows:

`CI=\hat p\pm z_(\alpha/2)* \sqrt{(\hat p(1-\hat p))/(n)}`

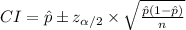
Here,

`\hat p` = sample proportion

`z_(\alpha/2)` = critical value

The width of a confidence interval (W) is:

`W=UL-LL\\=2* z_(\alpha/2)* \sqrt{(\hat p(1-\hat p))/(n)}`

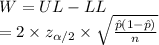
The value of W depends on three things,

1. Sample size (n)
2. Standard error
3. Confidence level ((1 - α)%)

The sample size is inversely proportional to the width of the interval. So, on increasing the sample size the width of the interval decreases and vice-versa.

The sample proportion is directly proportional to the width. Hence, making the standard error directly proportional to the width of the interval.

On increasing or decreasing the sample proportion the standard error increases or decreases. Hence, changing the width accordingly.

The critical value of z is also directly proportional to the width.

On increasing the confidence level the critical value increases and hence increasing the width of the interval. If a larger confidence interval is used the interval will be wider and if a smaller confidence interval is used the interval will be narrower.

The (1 - α)% confidence interval for the parameter implies that there is (1 - α)% confidence or certainty that the true parameter value is contained in the interval. If various samples of the same size is selected and the confidence interval is computed for each of these samples, then (1 - α)% of these confidence intervals will contain the true population parameter value.

Thus, the correct statements are (a), (c) and (d).