Question

Hugo and Viviana work in an office with eight other coworkers. Out of these 10 workers, their boss needs to choose a group of four to work together on a project.

(a) How many different working groups of four can the boss choose?
(b) Suppose Hugo and Viviana absolutely refuse, under any circumstances, to work together. Under this restriction, how many different working groups of four can be formed?

Answer 1

Answer:182 ways

Explanation:

Given

there are total of 10 workers in office

No of ways to select 4 workers out of 10 workers
`=^(10)C_4`

`=(10* 9* 8* 7)/(4* 3* 2* 1)=210`

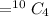
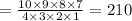
(b)If hugo and Viviana refuse to work together then

then no of ways in which hugo anf Viviana work together

`=^(8)C_2=28`

Therefore total no of ways in which Hugo and Viviana do not work together is
`=210-28=182\ ways`