Answer:
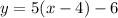 or
or
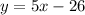
Explanation:
How we want the right side of the equation to look is entirely up to us, but the key to this problem is in getting y by itself. We basically want to turn this equation into a machine where we can punch in any value of x we want (it's independent because we have the freedom to choose (is free choice a thing? I'll leave that question to the philosophers)) and get out some value of y (the dependent variable, because it pops out from - or depends on - our choice of x).
So, we'll need to unwrap y from any operations connecting it to other numbers. In the equation
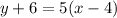 , y is connect to 6 by addition, so we can unwrap that addition with subtraction, making sure we subtract 6 from both sides to keep the equation balanced. This gives us
, y is connect to 6 by addition, so we can unwrap that addition with subtraction, making sure we subtract 6 from both sides to keep the equation balanced. This gives us
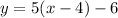 , which is perfect fine (and an incredibly useful form when you get to the topic of function transformations), but if we pick a value for x, we need to perform three different operations:
, which is perfect fine (and an incredibly useful form when you get to the topic of function transformations), but if we pick a value for x, we need to perform three different operations:
- Subtraction by 4
- Multiplication by 5
- Subtraction by 6
We can do better. If we simplify the right side, we can make our machine more efficient:
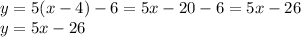
Now if we pick a value for x, we'll only need to
So if we pick x = 6, for instance:
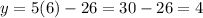 , and that's just a little bit nicer.
, and that's just a little bit nicer.