Question

A teacher has 30 students in a classroom. She has 6 seats in the front row. How many ways can she arrange her students to sit in the front row?

Answer 1

427,518,000 ways.

Explanation:

-This is a permutation problem of the form:

`P(n,r)=(n!)/((n-r)!)`

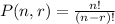
Where n is the number of objects and r is the number of objects taken at a time.

-Permutation is a linear order or sequence arrangement of a set's elements.

-The number of ways can therefore be calculated as:

`P(n,r)=(n!)/((n-r)!)\\\\\\=(30!)/((30-0)!)\\\\\\=427,518,000`

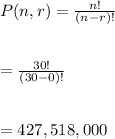
Hence, the 30 students can be arranged in 427,518,000 different ways.