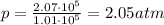Question

The pressure in car tires is often measured in pounds per square inch (lb/in.2), with the recommended pressure being in the range of 25 to 45 lb/in.2. Suppose a tire has a pressure of 30.0 lb/in.2. Convert 30.0 lb/in.2 to its equivalent in atmospheres. Express the pressure numerically in atmospheres.

Answer 1

2.05 atm

Step-by-step explanation:

The pressure exerted by a force is equal to the rate between the force exerted and the area over which the force is exerted:

`p=(F)/(A)`

where

p is the pressure

F is the force

A is the area

In this problem, we have the pressure written as

`p=30.0 (lb)/(in^2)`

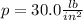
First, we need to convert this into SI units (Newton over squared meters, which is Pascal).

We have:

1 lb = 4.45 N

`1 in^2 = 6.45\cdot 10^(-4) m^2`

So the pressure converted into SI units is

`p=30.0 (ln)/(in^2)\cdot (4.45 N/lb)/(6.45\cdot 10^(-4) m^2/in^2)=2.07\cdot 10^5 Pa`

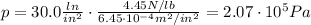
Now we know that 1 atmosphere is equivalent to

`1 atm = 1.01\cdot 10^5 Pa`

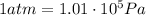
So we can convert this pressure into atmospheres:

`p=(2.07\cdot 10^5)/(1.01\cdot 10^5)=2.05 atm`