Question

What is the volume of the frustum? Express the answer in terms of π.

Answer 1

The answer is D

44.4π units^3

Answer 2

The volume of the frustum is:
`34.8 \, \pi \,units^3`

which corresponds to the third answer shown in the list of options

Explanation:

The image can be interpreted as an original tall cone of height 6.4 plus 6.8 (13.2) that was divided into two parts by chopping the smaller upper cone, and leaving the frustum (the volume of which we need to find). So, to estimate the volume of this frustum, knowing the general formula for the volume of a cone:

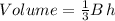`Volume= (1)/(3) B\,h` (where B is the area of the cone's base, and h its height)

we could calculate the volume of the larger cone, and subtract from it the volume of the upper smaller one.

For the area of the cone's base, recall call also that the area of a circle of radius R is given by:
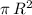`\pi\,R^2`, and therefore the formula for the volume of the cone can be written as:

`Volume= (1)/(3) \pi\,R^2\,h`

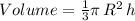
So, now the volume of the larger cone is:

`Volume= (1)/(3) \pi\,R^2\,h= (1)/(3) \pi\,3^2\,13.2=39.6\,\pi`

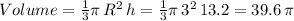
The volume of the smaller cone:

`Volume= (1)/(3) \pi\,R^2\,h= (1)/(3) \pi\,1.5^2\,6.4=4.8\, \pi`

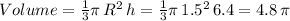
Therefore, the difference becomes:
`39.6\,\pi-4.8\,\pi=34.8\,\pi`

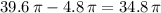
This is the volume of the frustum:
`34.8 \, \pi \,units^3`