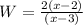Question

The area A of a rectangular garden is given by the expression2^2+ 2 − 12. The length L of the garden is given by the expression x2 - 9. Find an expression for the width W of the garden. (Recall that A = LW). What are the excluded values in this calculation and what do they represent in context?

Answer 1

`W=(2(x-2))/((x-3))`

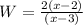
Explanation:

The correct question is

The area A of a rectangular garden is given by the expression 2x^2+2x− 12. The length L of the garden is given by the expression x^2 - 9. Find an expression for the width W of the garden. (Recall that A = LW). What are the excluded values in this calculation and what do they represent in context?

we know that

The area of a rectangular garden is given by the formula

`A=LW`

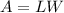
we have

`A=(2x^2+2x-12)\ units^2`

`L=(x^2-9)\ units`

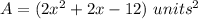
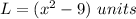
substitute

`(2x^2+2x-12)=(x^2-9)W`

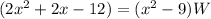
Solve for W

`W=((2x^2+2x-12))/((x^2-9))`

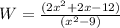
Find the roots of the quadratic equation of the numerator

The formula to solve a quadratic equation of the form

`ax^(2) +bx+c=0`

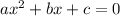
is equal to

`x=\frac{-b\pm\sqrt{b^(2)-4ac}} {2a}`

in this problem we have

`2x^2+2x-12=0`

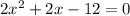
so

`a=2\\b=2\\c=-12`

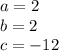
substitute in the formula

`x=\frac{-2\pm\sqrt{2^(2)-4(2)(-12)}} {2(2)}`

`x=\frac{-2\pm√(100)} {4}`

`x=\frac{-2\pm10} {4}`

`x=\frac{-2+10} {4}=2`

`x=\frac{-2-10} {4}=-3`

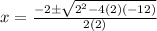
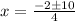
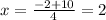
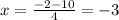
so

The roots are x=2 and x=-3

The quadratic equation in factored form is equal to

`2x^2+2x-12=2(x+3)(x-2)`

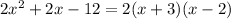
substitute in the above expression of W

`W=(2(x+3)(x-2))/((x^2-9))`

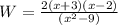
Rewrite the denominator as difference of squares

`(x^2-9)=(x+3)(x-3)`

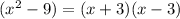
substitute

`W=(2(x+3)(x-2))/((x+3)(x-3))`

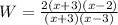
Remember that

In a quotient, the denominator cannot be equal to zero

so

x=-3 and x=3 are excluded values

x=3 represent a vertical asymptote

x=-3 is not included in the domain of the function because the length cannot be a negative number

Simplify

`W=(2(x-2))/((x-3))`