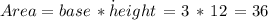Answer:
The Area of the rectangle is 36
Explanation:
One can use the vertices of the rectangle in coordinate form, by observing that (please see image attached):
(1) the distance between x-coordinates that share the same y-value give the length of the segments that define the horizontal sides of the rectangle,
(2) and the distance between y-coordinates that share the same x-value give the length of the segments that define the vertical sides of the rectangle,
Therefore, as an example of statement (1) above, the distance between the x-coordinates of : (-4,-3) and (-1,-3) which share the same "y-value" -3, is:
| -1 - (-4)| = |-1+4| = |3| = 3 which is the length of the horizontal side of the rectangle (the base of the rectangle).
As an example of statement (2), the distance between the y-coordinates of: ((-1,-3, and (-1,9) which share the same "x-value" -1, is:
| 9-(-3)| = |9+3|=|12|=12 which is the length of the vertical side of the rectangle (the height of the rectangle).
So, the area of the rectangle which is defined as the product of its base times its height, is given by: