Question

Boiling water, at 100 degrees Celsius, is placed in a freezer at 0 degrees Celsius. The temperature of the water is 50 degrees Celsius after 24 minutes. Find the temperature of the water to the nearest hundredth after 96 minutes

Answer 1

The temperature of the water after 96 minutes is
`6.25^oC`

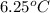
Explanation:

we know that

Newton's Law of Cooling states that the rate of change of the temperature of an object is proportional to the difference between its own temperature and the ambient temperature

so

`[T(t) - T_(a)] = [T(0) - T_(a)] e^(-kt)`

where

T(t) ----> is the temperature of the water at time t

T_a ---> is the ambient temperature (temp of the freezer)

T(0) ---> is the initial temperature of the water

k ---> is the cooling constant

we have

`T(0)=100^oC`

`T_a=0^oC`

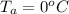
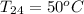`T_2_4=50^oC` ----> Temperature of the water at time 24 minutes

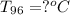`T_9_6=?^oC` ----> Temperature of the water at time 96 minutes

step 1

Find the value of k

substitute the given values

`[50 - 0] = [100 - 0}] e^(-k(24))`

`0.5=e^(-k(24))`

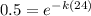
Applying ln both sides

`ln(0.5)=ln(e^(-k(24)))`

`ln(0.5)=-24k\\k=0.02888`

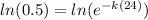
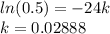
step 2

Determine
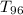`T_9_6` (Temperature of the water at time 96 minutes)

`[T_9_6 - T_(a)] = [T(0) - T_(a)] e^(-kt)`

substitute the given values

`[T_9_6 - 0] = [100 - 0] e^(-0.02888*96)`

`T_9_6= [100] e^(-0.02888*96)`

`T_9_6= 6.25^oC`