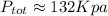Question

A graduated cylinder is half full of mercury and half full of water. Assume the height of the cylinder is 0.23 m and don't forget about atmospheric pressure. Calculate the pressure at the bottom of a graduated cylinder. (Provide answer to 3 significant digits.)

Answer 1

`P = 117.791\,kPa`

Step-by-step explanation:

The absolute pressure at the bottom of the cylinder is:

`P = P_(atm) + P_(man)`

`P = 101.325\,Pa + (1000\,(kg)/(m^(3))+13600\,(kg)/(m^(3)) )\cdot (9.807\,(m)/(s^(2)) )\cdot (0.115\,m)`

`P = 117790.953\,Pa`

`P = 117.791\,kPa`

Answer 2

`P_(tot)= 101325 Pa + 13600 (Kg)/(m^3) *9.8 (m)/(s^2) *0.23m`

`P_(tot)= 131979.4 Pa *(1Kpa)/(1000Pa)= 131.9794 Kpa`

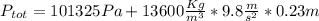
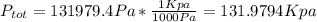
And using 3 significant digits we got
`P_(tot)\approx 132 Kpa`

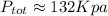
Step-by-step explanation:

For this case we have a cylinder with a height of h =0.23 m

We want to calculate the bottom presure at the bttom of the graduated cylinder, and the formula for the total pressure would be given by:

`P_(tot)= P_(atm) + \rho_(Hg) g h`

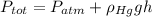
For this case we have the following info:

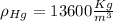`\rho_(Hg) = 13600 (Kg)/(m^3)` the density for the mercury

`h =0.23 m` the heigth of the cylinder

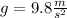`g = 9.8 (m)/(s^2)` represent the gravity

`P_(atm)= 101325 Pa` the atmospheric pressure assumed.

And replacing we got:

`P_(tot)= 101325 Pa + 13600 (Kg)/(m^3) *9.8 (m)/(s^2) *0.23m`

`P_(tot)= 131979.4 Pa *(1Kpa)/(1000Pa)= 131.9794 Kpa`

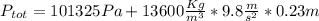
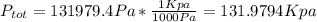
And using 3 significant digits we got
`P_(tot)\approx 132 Kpa`