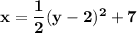Question

Part 1: Use the information provided to write the vertex form equation of each parabola.

1. Vertex: (9, 10)
Focus: (9, 19/2)

2. Vertex: (4,1)
Focus: (17/4, 1)

3. Vertex: (7,2)
Focus: (15/2, 2)

Answer 1

Answer:
`\bold{1.\quad y=-(1)/(2)(x-9)^2+10}`

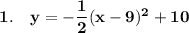
2. x = (y - 1)² + 4

`\bold{3.\quad x=(1)/(2)(y-2)^2+7}`

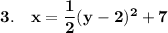
Explanation:

Notes: The vertex form of a parabola is y = a(x - h)² + k or x = a(y - k)² + h

• (h, k) is the vertex
• p is the distance from the vertex to the focus

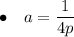
`\bullet\quad a=(1)/(4p)`

1)

`\text{Vertex}=(9, 10)\qquad \text{Focus}=\bigg(9,(19)/(2)\bigg)\\\\\text{Given}:(h, k)=(9, 10)\\\\\\p=focus-vertex=(19)/(2)-(20)/(2)=(-1)/(2)\\\\\\a=(1)/(4p)=(1)/(4((-1)/(2)))=(1)/(-2)=-(1)/(2)\\`

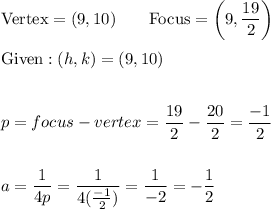
Now input a = -1/2 and (h, k) = (9, 10) into the equation y = a(x - h)² + k

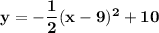
`\bold{y=-(1)/(2)(x-9)^2+10}`

*****************************************************************************************

2)

`\text{Vertex}=(4, 1)\qquad \text{Focus}=\bigg((17)/(4),1\bigg)\\\\\text{Given}:(h, k)=(4, 1)\\\\\\p=focus-vertex=(17)/(4)-(16)/(4)=(1)/(4)\\\\\\a=(1)/(4p)=(1)/(4((1)/(4)))=(1)/(1)=1\\`

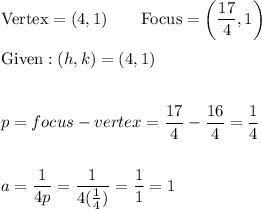
Now input a = 1 and (h, k) = (4, 1) into the equation x = a(y - k)² + h

x = 1(y - 1)² + 4 → x = (y - 1)² + 4

*****************************************************************************************

3)

`\text{Vertex}=(7, 2)\qquad \text{Focus}=\bigg((15)/(2),2\bigg)\\\\\text{Given}:(h, k)=(7, 2)\\\\\\p=focus-vertex=(15)/(2)-(14)/(2)=(1)/(2)\\\\\\a=(1)/(4p)=(1)/(4((1)/(2)))=(1)/(2)`

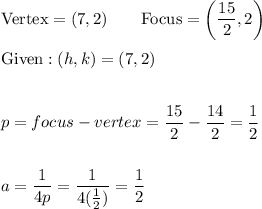
Now input a = 1/2 and (h, k) = (7, 2) into the equation x = a(y - k)² + h

`\bold{x=(1)/(2)(y-2)^2+7}`