Answer:
A parabola opens downward with vertex at (1,20)
Explanation:
The function that models the height of bag of candies is
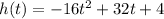
The graph of this function is a parabola that opens downward.
To find the maximum height of the candy bag, we complete the squares to obtain the vertex form of the function.
Factor -16 to get;
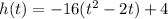
Add and subtract the square of half the coefficient of t.
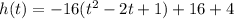
Factor the perfect square trinomial:
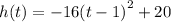
The vertex is (1,20)
This means the maximum height after 1 second is 20 feet.