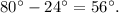Therefore, the difference of arc measures
 is
is
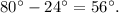
To solve this problem, we'll use the fact that the angle formed by two secants intersecting outside of a circle is equal to half the difference of the measures of the arcs that the secants intercept.
Given:
- The measure of angle

- The measure of arc
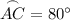
- The measure of arc
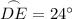
The formula to find the angle formed by two intersecting secants is:
![\[ m \angle ABC = (1)/(2) (m \overset{\frown}{AC} - m \overset{\frown}{DE}) \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/l87rm9ei78kt2iic87tp2oz3l5mtceggp4.png)
Now, we can calculate step by step:
1. Substitute the given values into the formula:
![\[ 28 = (1)/(2) (80 - m \overset{\frown}{DE}) \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/y7u78isvzku3h8o7pfomtyiz3gygk2bgm6.png)
2. Double both sides to eliminate the fraction:
![\[ 56 = 80 - m \overset{\frown}{DE} \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/6k5p3rx8fmt9am8juz9m0wtchd20ql9nzt.png)
3. Solve for
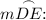
![\[ m \overset{\frown}{DE} = 80 - 56 \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/jdymdximt7wj3qpwqn5ww5tfg7g07z8xmb.png)
![\[ m \overset{\frown}{DE} = 24^\circ \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/pirmi3wr9pbts7m2zuvz8foxccb4676sbc.png)
Since
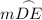 is already given as
is already given as
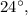 the calculation confirms that the given values are consistent with the properties of intersecting secants.
the calculation confirms that the given values are consistent with the properties of intersecting secants.
Therefore, the difference of arc measures
 is
is