Question

Super urgent can someone help me with this i spent a lot of points and i received a fake answer

Answer 1

(a) 3, 2, -3, -7, -12, -18, -25, -33 etc.

(b) -44, -12, -4, 4, 12, 44

Explanation:

Integer: whole numbers (including negatives)

To factor a quadratic in the form
`ax^2+bx+c`

• Find 2 two numbers (d and e) that multiply to
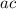  `ac` and sum to
  `b`
• Rewrite
  `b` as the sum of these 2 numbers:
  `d+e=b`
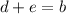
• Factorize the first two terms and the last two terms separately, then factor out the comment term.

Question (a)

Given quadratic:
`kx^2+5x+2`

`\implies a=k, b=5\: \textsf{and}\:c=2`

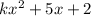
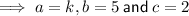
You don't have to do this, but it is helpful to first find the range of k. To do this, use the discriminant
`b^2-4ac`.

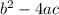If the quadratic has 2 real roots then
`b^2-4ac > 0`

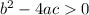
If the quadratic has 1 real root then
`b^2-4ac = 0`

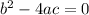
Therefore, set the discriminant to ≥ 0

`\implies 5^2-4(k)(2)\geq 0`

`\implies 25-8k\geq 0`

`\implies -8k\geq -25`

`\implies 8k\leq 25`

`\implies k\leq 3.125`

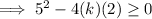
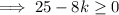
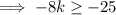
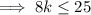
As k is an integer,
`k\leq 3`

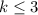
Given quadratic:
`kx^2+5x+2`

`\implies ac=k \cdot 2=2k`

`\implies d+e=5`

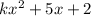
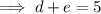
So we need to find pairs of numbers that sum to 5 and multiply to a (negative or positive) even number, since
`ac=2k`

2 + 3 = 5 and 2 · 3 = 6 ⇒ 2k = 6 ⇒ k = 3

1 + 4 = 5 and 1 · 4 = 4 ⇒ 2k = 4 ⇒ k = 2

-1 + 6 = 5 and -1 · 6 = -6 ⇒ 2k = -6 ⇒ k = -3

-2 + 7 = 5 and -2 · 7 = -14 ⇒ 2k = -14 ⇒ k = -7

-3 + 8 = 5 and -3 · 8 = -24 ⇒ 2k = -24 ⇒ k = -12

-4 + 9 = 5 and -4 · 9 = -36 ⇒ 2k = -36 ⇒ k = -18

-5 + 10 = 5 and -5 · 10 = -50 ⇒ 2k = -50 ⇒ k = -25

-6 + 11 = 5 and -6 · 11 = -66 ⇒ 2k = -66 ⇒ k = -33

etc.

Therefore, possible values of k are:

3, 2, -3, -7, -12, -18, -25, -33 etc.

-------------------------------------------------------------------------------------------

Question (b)

Given quadratic:
`9x^2+kx-5`

`\implies a=9, b=k\: \textsf{and}\:c=-5`

`\implies ac=9 \cdot -5=-45`

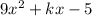
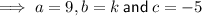
Find factors of -45:

• 1 and -45
• -1 and 45
• 3 and -15
• -3 and 15
• 5 and -9
• -5 and 9

As
`a+c=k`:

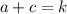• 1 + -45 = -44
• -1 + 45 = 44
• 3 + -15 = -12
• -3 + 15 = 12
• 5 + -9 = -4
• -5 + 9 = 4

Therefore, all possible values of k are -44, -12, -4, 4, 12, 44