Question

The rectangle shown has length AC = 32, width AE = 20, and B and F are midpoints of AC and AE , respectively. The area of quadrilateral ABDF is

Answer 1

Option A.

Explanation:

Given question is incomplete: please find the question in the attachment.

Area of quadrilateral ABDF = Area of AECD - Area of ΔBCD - Area of ΔDEF,

Since, area of AECD = (AC × AE)

Area of ΔBCD =
`(1)/(2)(BC* CD)`

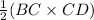
Area of ΔDEF =
`(1)/(2)(EF* ED)`

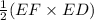
= (AC × AE) -
`(1)/(2)(BC* CD) - (1)/(2)(EF* ED)`

= (32 × 20) -
`(1)/(2)(16* 20) - (1)/(2)(10* 32)`

= 640 - 160 - 160

= 640 - 320

= 320 square unit

Therefore, Option A is the correct option.