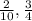Answer:
The product of two fractions can be calculated as follows:
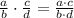
So, the numerator is the product of the numerators of the two fractions, and the denominator is the product of the denominators of the two fractions.
In this problem, we know that the product is 6/40, so:

This means:
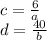
So we just need to find 2 pairs of numbers a, b to make c and d integers.
The first choice we use is:
a = 3
b = 2
So we get:
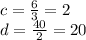
So the first pair of fractions is
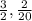
The second choice we use is:
a = 2
b = 10
So we get:
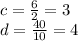
So the second pair of fractions is