Answer:
There are 48 coins in total.
Shawna found:
12 Pennies.
12 Nickels.
16 Dimes.
And 8 Quarters.
Explanation:
We will let
 denote the total amount of coins.
denote the total amount of coins.
We know that the total worth of the coins were $4.32.
One-fourth of the found coins are pennies. Hence:
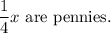
Since pennies are worth $0.01 each, the worth will be:
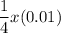
Similarly, we know that one-sixth of the found coins are quarters. Quarter are worth $0.25. So, the total worth in quarters is:
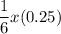
We have 1.5 times as many nickels as quarters. Therefore, the amount of nickels we have is:
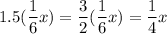
Or one-fourth of the total amount.
Since each nickel is worth $0.05, the total worth in nickels is:
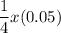
We will now need to determine the amount to dimes. Notice that 1/4 of the total amount of coins were pennies, 1/6 were quarters, and another 1/4 were nickels. Therefore, the amount of coins that were dimes n must be the remaining fraction of the total amount of coins. In other words, the fraction that were dimes is:

Evaluate for n. Let 100% equal 1. Hence:
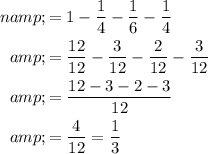
Therefore, 1/3 of the coins were dimes.
Since dimes are worth $0.10, the total worth in dimes are:
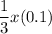
The total worth of all the coins found was worth $4.32. Therefore:
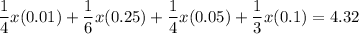
Solve for
 , the total amount of coins. First, let’s multiply everything by 100 to remove the decimals. Hence:
, the total amount of coins. First, let’s multiply everything by 100 to remove the decimals. Hence:
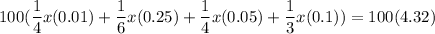
Distribute:
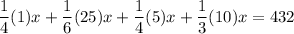
Now, let’s multiply everything by 12 to remove the fractions. 12 is the LCM of 4, 6, and 3. Hence:
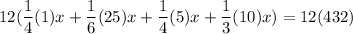
Distribute:
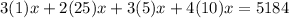
Multiply:
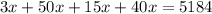
Combine like terms:

Divide both sides by 108. Hence, the total amount of coins are:
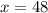
1/4 of the total coins are pennies. Hence, there are 1/4(48) or 12 pennies.
1/6 of the total coins are quarters. Hence, there are 1/6(48) or 8 quarters.
As we determined, 1/4 of the total coins are also nickels. Hence, there are 1/4(48) or 12 nickels.
Finally, as we determined, 1/3 of the total coins are dimes. Hence, there are 1/3(48) or 16 times.