Question

An arc subtends a central angle measuring \dfrac{\pi}{2}

2
π
​
start fraction, pi, divided by, 2, end fraction radians.
What fraction of the circumference is this arc?
of the circumference

Answer 1

It is 1/4th of the circumference

Explanation:

It is the correct answer on khan academy

Answer 2

Arc Length is 1/4th of the circumference .

Explanation:

Here we need to find fraction of the circumference is this arc when An arc subtends a central angle measuring
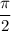`(\pi)/(2)` radians ! Let's find out :

We know that circumference of an arc subtending a central angle of x is :

⇒
`Arc = (Angle)/(360)(2\pi r)`

⇒
`Arc = ((\pi)/(2))/(360)(2\pi r)`

⇒
`Arc = (90)/(360)(2\pi r)`

⇒
`Arc = (90)/(90(4))(2\pi r)`

⇒
`Arc = (1)/(4)(2\pi r)`

⇒
`Arc = (1)/(4)(Circumference)`

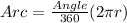
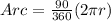
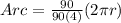
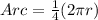
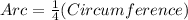
Therefore , Arc Length is 1/4th of the circumference .