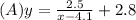Question

Which of these functions has a domain of all real numbers except x=4.1?

A. y=2.5x−4.1+2.8


B. y=2.8x+4.1−2.5


C. y=4.1x−2.8+2.5


D. y=4.1x−2.5+2.8

Answer 1

`(A)y=(2.5)/(x-4.1) + 2.8`

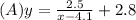
Explanation:

In the expressions, the value at which the domain of the function will be the set of all real numbers except x=4.1 is the value at which 4.1 makes the denominator equal to zero, i.e makes the fraction undefined.

Given the options

`(A)y=(2.5)/(x-4.1) + 2.8`

Setting the denominator to zero, x-4.1=0, x=4.1. The fraction is undefined at x=4.1

`(B)y=(2.8)/(x+4.1) -2.5`

Setting the denominator to zero, x+4.1=0, x=-4.1. The fraction is undefined at x=-4.1

`(C)y=(4.1)/(x-2.8) +2.5`

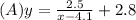
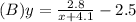
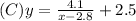
Setting the denominator to zero, x-2.8=0, x=2.8. The fraction is undefined at x=2.8

`(D)y=(4.1)/(x-2.5) +2.8`

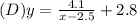
Setting the denominator to zero, x-2.5=0, x=2.5. The fraction is undefined at x=2.5

Therefore, function that has a domain of all real numbers except x=4.1 is:

`(A)y=(2.5)/(x-4.1) + 2.8`