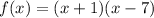Answer:
Explanation:
For a quadratic function to have a vertex with an x-coordinate of 3, then
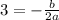
Let a=1, then we have
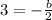
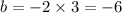
So now our equation becomes:
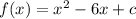
We now find two factors of c that add up to -6.
Let these factors be 1, and c.
Then

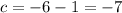
Therefore the factors are :
1 and -7.
The function becomes:
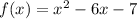
The factored form is