Question

A private party wants to fill the Gold Ballroom with rows of round tables. The tables are 4 feet in diameter, and each table has to be 5 feet away from the wall and from other tables. How many tables can you fit?

The area of the Ballroom is 1288 ft.

Answer 1

• 9 tables

Step-by-step explanation:

Take first the direction along one wall. If there are n tables they occupy a length of n × 4 feet.

There are (n - 1) 5-feet spaces between them. That is additional 5 × (n - 1) feet.

Also, each table on the ends are separated 5 feet from the wall. That is an additional 5 feet + 5 feet = 10 feet length.

The total length occupied by n tables is 4n + 5(n-1) + 10 = 4n + 5n - 5 + 10 =9n + 5 feet

The situation is the same in the direction of the perpendicular walls: 9n - 5 feet.

Thus, the area is (9n + 5)² = 1288 ft²

Solve the equation:

`(9n+5)^2=1288ft^2`

`(9n+5)=√(1,288ft^2)`

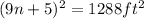
9n + 5 = 35.89

9n = 30.89

n = 3.4

You must round to whole number of tables. That is 3 tables in one direction and 3 tables in the other direction.

Then, the number of tables is 3 × 3 = 9 ← answer