Question

You are going to complete several meteorological tests using a large weather balloon. You wish to check the temperature at 3000 meters altitude. You want to make sure the balloon will not burst before it reaches that height. Some calculations are needed. The balloon manufacturer guarantees the balloon up to 47.0 Liters in size. Will the balloon make it to the necessary height without bursting? The temperature at ground level is 20 C. The pressure is 765 mmHg. The volume of the balloon prior to release is 30.0 Liters. It is filled with helium, which is lighter than air. For both calculations you will be using PV =nRT. Show all work for any credit. 1. Calculate the amount in grams of helium in the balloon. Hint remember n = moles 2. Can the balloon ascend to 3000 meters without bursting? The temperature and pressure at 3000 meters was measured at Temp = 6.0 C, Pressure = .565 atm For both calculations you will be using PV =nRT. Show all work for any credit.

Answer 1

• Question 1: You cannot make sure the ballon will not burst before it reaches 3,000m altitude because the volume will exceed 47.0 liters

• Question 2: 5.0 g

Step-by-step explanation:

1. Data

• Maximum volume of the balloon: 47.0 liters

At 3,000 m:

• Temperature at 3,000 m, T₁: 6.0ºC

• Pressure at 3,000m, P₁: 0.565atm

• Volume, V₁ = ?

At ground:

• Temperature at ground, T₂: 20ºC

• Pressure at ground, P₂: 765mmHg

• Volume at ground, V₂: 30.0 liters

Questions:

• Will the balloon's volume be more than 47.0 liter?

• Amount in grams of helium in the ballon:?

2. Unit conversions:

a) Convert P₂ to atm:

• P₂ = 765mmHg × 1 atm/760.0mmHg = 1.00657895atm

b) Convert the temperatures to kelvin:

• T₁ = 6.0 + 273.15 = 279.15K

• T₂ = 20 + 273.15 = 293.15K

3. Solution

Question 1.

Calculate the final volume of the balloon:

Since the number of moles of helium gas inside the balloon remains unchanged, pV = nRT yields the combined gas law:

`(P_1V_1)/(T_1)=(P_2V_2)/(T_2)`

From which you can solve for V₁ and compute it:

`V_1=(P_2V_2T_1)/(P_1T_2)`

`V_1=(1.00657895atm\cdot 30.0liter\cdot 279.15K)/(0.565atm\cdot 293.15K)`

`V_1\approx51liters`

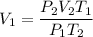
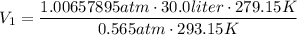
Then, the volume of the balloon will exceed the gurantee of the manufacturer.

Question 2.

a) Calculate the number of moles of helium

`pV=nRT`

`n=(pV)/(RT)`

`n=(1.00657895atm* 30.0liter)/(0.08206atm\cdot liter/(K\cdot mol)* 293.15K)`

`n=1.2558mol`

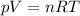
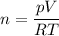
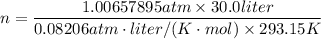
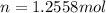
b) Calculate the mass in grams of helium

Use the atomic mass of helium: 4.003g/mol

• mass = number of moles × molar mass

• mass = 1.2558mol × 4.003g/mol = 5.02g

Rounding to 2 significant figures: 5.0g