Question

John stands 150 meters from a water tower and sights the top at an angle of elevation of 36º. If John's eyes are 2 meters above the ground, how tall is the tower? Round to the nearest meter.

Answer 1

The height of tower
`DB=111\ meters`.

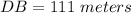Explanation:

Diagram of the given scenario is shown below.

Given that,

Distance between John and tower is
`CE=150 \ meters`.

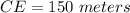Angle of elevation to the top of the tower is
`\angle DEC=36`°.

Height of John is
`CB=2\ meters`.

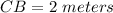To Find: Height of the tower
`DB`.

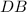So,

In triangle ΔDCE,

`Tan`(∠
`DEC)= (DC)/(CE)`

`Tan (36)= (DC)/(150)`

`DC= tan(36)* 150`

`DC=108.98\ meters`

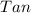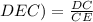
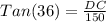
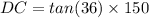
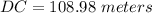
Now,

To calculate the height of tower we have

`DB=DC+CB`

`DB=108.98+2`

`DB=110.98\ meters` ≈
`111 \ meters`

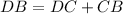
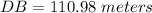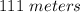
Therefore,

The height of tower
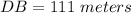`DB=111\ meters`.