Question

The area of a playground is 20 yd.². The length of the playground at five times longer than it's worth. Find the length and the width of the playground.

Answer 1

Length = 5 yards and Width = 2 yards.

Explanation:

Given:

The area of a playground is 20 yd.²

The length of the playground at five times longer than it's width.

Question asked:

Find the length and the width of the playground.

Solution:

Let width of the playground =
`x`

Then, length of the playground =
`5x`

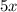
As we know:

`Area \ of\ rectangle=length* width`

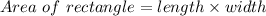
`20=5x* x\\20=5x^(2) \\Dividing\ both \ sides\ by\ 5\\\\ x^(2) =4\\Taking\ root\ both\ sides\\ \\ \sqrt[2]{x^(2) } =\sqrt[2]{4} \\ \\ x=\sqrt[2]{2*2} \\ \\ x=2`

By substituting the value:-

width of the playground =
`x` = 2 yards

length of the playground =
`5x` =
`5*2=10\ yards`

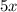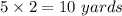
Therefore, the length and the width of the playground is 5 yards and 2 yards.